CENTRE NATIONAL D'ETUDES SPATIALES

Après avoir examiné, dans le chapitre 3, les perceptions sensorielles liées au phénomène allégué par Rosine et par Lucille, je vais tenter de reconstituer, à titre hypothétique, ce qu'aurait pu être un phénomène physique ayant eu l'apparence décrite par les témoins. Ce projet appelle les commentaires suivants :

(1) Je retiens en priorité l'hypothèse physique parce qu'elle possède des avantages irremplaçables dès lors qu'on désire effectuer une étude quantitative. Celle-ci gagne immédiatement en simplicité et en spécificité si on suppose à l'origine des perceptions alléguées par les témoins, un objet doté de caractéristiques géométriques. L'analyse, initialement limitée à des perceptions, peut alors être poursuivie dans le but de préciser la localisation et l'extension spatiale de l'objet hypothétique.

(2) L'hypothèse, telle que je l'utiliserai, ne suppose absolument rien d'autre que ces propriétés physiques élémentaires ( localisation, extension, impénétrabilité ). Je ne supposerai bien entendu rien ( je n'en ai nul besoin ) quant à la nature de l'objet ainsi posé à l'origine de l'expérience vécue par les témoins. Je n'entends pas m'engager dans ce débat, non que je le considère comme sans importance, mais parce que ce n'est pas le lieu de le discuter et qu'il importe de ne pas confondre les niveaux d'analyse.

(3) L'utilisation de l'hypothèse physique, comme base d'analyse, ne signifie pas que je la considère comme seule possible d'autres interprétations, d'autres lectures du cas peuvent être utilement proposées.

(4) Le cas utilisé n'est pas le meilleur qu'on aurait pu souhaiter. Les insuffisances proviennent d'une part, des témoins eux mêmes, d'autre part des enquêtes et des techniques encore imparfaites utilisées pour "extraire" une information que les témoins possèdent sous une forme brute mais qu'ils ne sont pas toujours capables d'exprimer clairement. On peut donc considérer l'analyse effectuée comme un exercice pratique destiné à étudier les difficultés et les limites de cette approche en vue de l'étude d'autres cas plus féconds.

(5) Il est non seulement légitime mais nécessaire de tenter l'analyse des données disponibles à la limite de ce qu'elles peuvent fournir à condition de conserver présent à l'esprit l'incertitude sur les grandeurs estimées et les hypothèses sur lesquelles reposent ces estimations. Si ces précautions sont prises tant par l'auteur que par le lecteur, il ne devrait y avoir qu'avantage à réfléchir suivant ces lignes.

2 - METHODES

L'étude complète d'une observation nécessite une connaissance approfondie des lieux où elle s'est déroulée. Il m'a ainsi fallu déterminer non seulement la position exacte des points remarquables mais aussi leur altitude et la hauteur de diverses constructions et obstacles. Or, il s'est avéré que le plus grande partie des détails topographiques indispensables ne figuraient pas sur le matériel cartographique pourtant très abondant dont je disposais ( sans même parler des altitudes et hauteurs ) ou que la précision de leur localisation y laissait à désirer, et que même pour les aspects représentés, l'utilisation de ces cartes était rendue très mal commode et imprécise par la diversité de leurs échelles.

Dans ces conditions, force m'a été de reprendre le problème de la description topographique au départ et de me servir des cartes et plans cadastraux comme simple appoint seulement. Les difficultés rencontrées ne sont pas particulières au cas étudié mais elles se rencontreront à nouveau dans l'analyse de la plupart des cas "d'atterrissages" qui seront menés à l'avenir suivant, ces lignes. Aussi est-il utile de décrire rapidement les techniques utilisées pour faciliter leur réutilisation et leur amélioration.

2.1. Prises de vue et tirages

Une enquête sur le terrain devant s'opérer dans des délais généralement courts, l'utilisation de la photographie semble le moyen idéal de collecter rapidement un matériel exhaustif et susceptible d'une analyse ultérieure détaillée même par les chercheurs n'ayant pas été sur les lieux. Son inconvénient majeur est d'être tributaire des conditions atmosphériques.

Présentement, les vues ont été prises à l'aide d'un objectif de focale f - 28 mm sur négatif noir et blanc 24 x 36 min. Les vues ont été prises en 3 panoramiques à 360° ( en O, P'3 et près du carrefour des chemins départementaux, chap. 3, fig. 3.2. ), 2 semi-panoramiques à 180° ( en P1 et P4 ) et en plusieurs points isolés ( P2, P3, etc. ). Dans un panoramique, les vues successives se recouvrent partiellement. La verticalité de l'axe de rotation de l'appareil sur son pied a été contrôlée avec un soin particulier au moyen d'un niveau à bulle. Les points de prise de vue ont été choisis de manière à être ultérieurement situés avec précision.

Un certain nombre de distances remarquables a été relevé au double-décamètre de manière à servir de contrôle lors du dépouillement des épreuves.

Les épreuves ont été tirées à un grandissement G = 5. Les bords du négatif ont été laissées apparents de manière à permettre un contrôle de C à posteriori. Les épreuves sont donc toutes au format 12 x 18 cm.

2.2. Mesures sur les épreuves

Une liste de détails remarquables, dont il importait de connaître les caractéristiques géométriques, a été établie et chacun d'eux annoté symboliquement sur les épreuves.

Les coordonnées des bases et des sommets des détails choisis ont été mesurés par rapport aux bords de l'épreuve puis exprimés dans un repère xy, désignant le centre de l'épreuve.

2.3. Détermination des positions

Le dépouillement des épreuves relatives à un même panoramique permet de déterminer les directions de tous les détails qui y apparaissent. Le chevauchement des vues successives permet de passer sans discontinuité de l'une à l'autre. Pratiquement, les directions sont reportées sur la carte en y traçant un triangle isocèle dont le sommet est situé au point de prise de vue 1, dont la hauteur est égale à la focale de l'objectif multiplié par le grandissement de l'épreuve ( ici 28 x 5 = 140 mm ) et la base égale à la largeur de l'épreuve ( ici 180 mm ) ; les abscisses x mesurées sur l'épreuve sont reportées sur la base, les directions s'en déduisent immédiatement.

Pour situer correctement le point central 2 d'un second panoramique et orienter correctement sa première épreuve, il faut connaître, par exemple, la distance qui le sépare de 1 et la distance de ces points à un repère visible sur les deux panoramiques. ( D'autres solutions sont d'ailleurs possibles et dans tous les cas, on peut résoudre le problème par itération à l'aide de 3 panoramiques ). La position des différents détails est alors donnée par l'intersection de leurs directions issues de 1 et 2. La précision de la méthode n'est évidemment pas la même en tout point...

Le résultat de ce travail est la figure 3.2. du chapitre 3.

2.4. Détermination des altitudes et hauteurs

Considérons un point M du paysage, visible en M' sur une épreuve de grandissement G. Il s'agit de déterminer l'altitude H du point M au dessus du plan horizontal passant par l'objectif de focale f, connaissant d'une part la distance D entre A et la projection P de M sur le plan horizontal ( distance mesurée sur la plan établi précédemment ), et d'autre part les coordonnées ( x,y ) de M' dans le repère d'origine ? lié à l'épreuve. On montre ( fig. A3.1 ) que H est donnée par la relation :

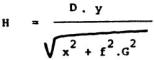
FIGURE A3 .1. : DETERMINATION DE L'ALTITUDE H D'UN OBSTACLE M

L'altitude est calculée au-dessus du plan horizontal passant par l'objectif de focale f de l'appareil de prise de vue, à partir d'une épreuve de grandissement G.

Le plan horizontal passant 1 m environ au dessus de la partie supérieure de la trace O a été pris comme niveau zéro. Son altitude vraie est 240 m environ.

Il est aisé de calculer de cette manière l'altitude H des sommets des obstacles ( maisons, poteaux, arbres, ... ), car ils sont en général nettement visibles sur les épreuves. Les bases par contre sont beaucoup moins nettes et l'altitude du sol ne peut pas être déterminée en chaque point. Les hauteurs des obstacles par rapport au sol ^H sont donc moins précises, ce qui est de peu de conséquence pour l'étude qui suit.

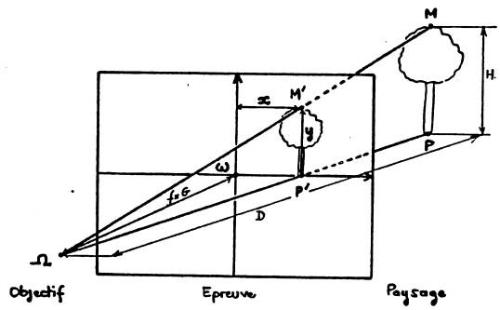
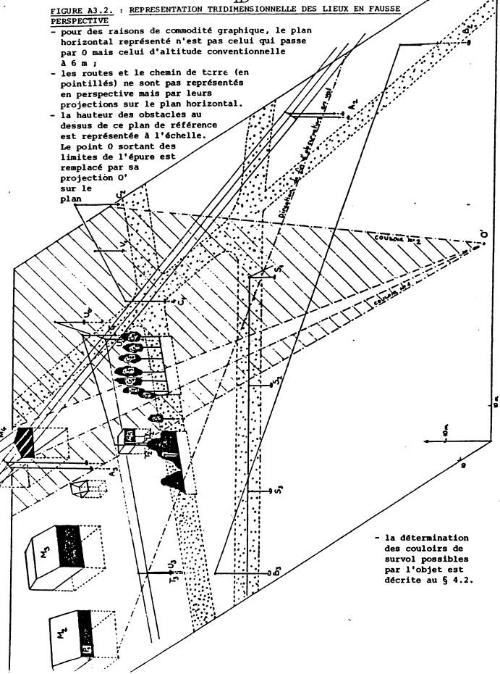
L'utilisation conjointe de l'ensemble de ces données quantitatives a permis de réaliser une représentation tridimensionnelle des lieux ( fig. A3.2 ).

3 - L'OBJET A L'ARRET : POSITION ET DIMENSION

3 .1. Position

La position de l'objet dans sa phase immobile peut être aisément déterminée par triangulation. Prenons par exemple, les déclarations de Rosine en 1979. De P3, elle aurait vu l'objet dans la direction exacte de la trace O mais à une distance indéterminée. Elle l'aurait de nouveau aperçu de P4, point situé à plus de 100 m de P3, dans une direction qui n'est pas connue de manière aussi précise. On peut cependant en déduire que le point d'intersection des 2 directions est à 125 ± 17 m de P3 et à 172 ± 12 m de P4 en prenant les poteaux B3 et T4 comme bornes extrêmes. Ce résultat est remarquable car le point O ( trace ) est précisément situé à 126 m de P3 et 175 m de P4. Il y aurait donc identité des localisations du phénomène et de la trace.

Cette conclusion nécessite cependant, pour être probante, que les déterminations de la position de la trace d'une part et des directions d'observation d'autre-part, soient totalement indépendantes. Or, nous avons vu à l'annexe 2 que, si cette indépendance était probable en P4, elle était problématique en P2 et en P3, sans mentionner P'3 dont le statut est incertain. Faut-il alors abandonner la conclusion précédente et par conséquent une partie importante des éléments qui confèrent validité et intérêt au cas étudié ?

Un jugement aussi sévère ne me semble pas justifié. En dépit des incertitudes signalées qui portent sur des aspects très spécifiques, les résultats suivants semblent devoir être retenus :

Rosine a observé le phénomène allégué à partir d'un point situé entre P3 et P'3 car toutes ses déclarations convergent. L'incertitude sur sa position est donc ± 1,5 m au maximum.

Elle est même plus faible si, en dépit des restrictions faites, on admet une localisation proche de P3 comme plus probable qu'une autre dans la mesure où elle correspond aux premières déclarations de Rosine.
L'observation a eu lieu au travers de l'ouverture entre le poteau T2, près de l'abri de chantier M5, et le bottier EDF E ou l'extrémité de la haie, car dans toutes les autres directions la vue est obstruée.

La zone d'incertitude la plus grande qui s'en déduit est limitée par la direction P3E (à droite) et P'3 T2 ( à gauche ) d'une part, P4 B3 ( en bas ) et P4 T4 ( en haut ) d'autre part. Le quadrilatère ainsi dessiné ( fig. A3.3 ) inclut le point O. L'axe médian issu de P3 P'3 intersecte l'axe médian issu de P4 en un point O' situé à moins de 12 m de O.

Une utilisation critique des données ne retenant que les fourchette d'incertitude les plus grandes conduit donc substantiellement au même résultat : le phénomène stationnaire a bien été observé par Rosine au voisinage de O.

En conclusion le lien, établi dès l'origine, entre la trace constatée en O et le phénomène allégué, ne serait pas fortuit. Il semble donc possible d'admettre que le phénomène était bien au dessus de la trace O et à une altitude très faible en raison du site d'observation. Si cette suggestion est exacte, le phénomène au sol serait resté immobile durant les déplacements de Rosine entre sa maison, le portique et la maison de Lucille ( 1 mm 1/2 environ ).

Pour simplifier les calculs qui suivent, j'admettrai purement et simplement une immobilisation de l'objet hypothétique en O exactement.

3.2. Dimensions

3.2.1. Dimension horizontale L

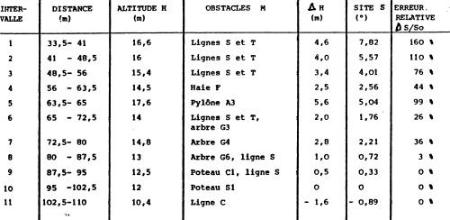
Si l'on admet que l'objet stationnaire était en O, sa distance au témoin s'établit à 125 m environ, ce qui permet de convertir les dimensions angulaires en dimensions linéaires ( tableau 1 ).

TABLEAU 1 : Longueur de l'objet

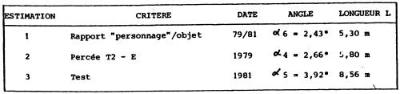
FIGURE A3.3. : Détermination par triangulation de la position de l'objet à l'arrêt

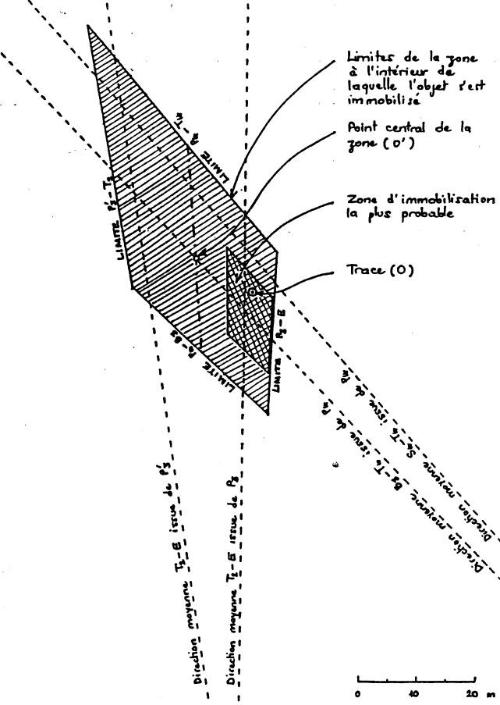
La méthode de dérivation des 2 dernières estimations a été décrite au chapitre 3 ( § 6 ). Quant à la première, elle est obtenue à partir d'une estimation de la taille de la silhouette lumineuse ( 1,65 m ) obtenue par comparaison à un enquêteur situé en O, et du rapport "hauteur de la silhouette : longueur de l'objet", rapport qui a été évalué à 1 : 3,2 en faisant la moyenne des rapports de 1979 ( 1 : 3,08 ) et de 1981 ( 1 : 3,3 ) ( chap. 3.§7 ).

Discussion :

Compte tenu des hésitations de Rosine dans l'exécution du test, la dernière estimation doit être tenue pour moins fiable que la seconde ( chap. 3 §6.2 ) et que la première qui, en dépit de son caractère indirect, est assez bien étayée.

Dans ces conditions, la dimension angulaire de l'objet au sol la plus probable est la moyenne de ₄ et de ₆ soit 2,55° ce qui correspond à une longueur L de 5,5 m environ.

Il convient de s'interroger sur la fourchette de validité d'une telle évaluation. L'estimation n°2 se sert de la percée comme repère, le problème étant de savoir si l'objet était en réalité plus petit ou plus grand. Admettons pour fixer les idées, une erreur de 30 % dans un sens ou dans l'autre. L'estimation n°1 se fonde d'une part sur la comparaison de la hauteur de la silhouette à celle d'un homme et d'autre part sur la comparaison de l'objet à cette silhouette. On peut considérer une erreur de 15 % sur ces rapports comme un maximum soit une erreur cumulée de 30 %. On aurait donc :

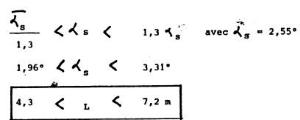
3.2.2. Dimension verticale H

Le rapport H/L a été évalué à 0,38 sur l'objet en vol ( chap. 3 §5.1 ). La hauteur la plus probable de l'objet serait donc :

H = 2,1 m

dont 1,4 pour la partie supérieure et 0,7 pour l'inférieure. Une erreur de 15 % sur ce rapport conduit à la fourchette :

1,8 < H < 2,4

4 - L'OBJET EN VOL : TRAJECTOIRE ET VITESSE

4.1. Détermination de la trajectoire d'après le témoignage de Rosine

4.1.1. Distance

La plus grande dimension de l'objet étant connu de manière approximative, il est possible de déduire sa distance D. au témoin à partir de sa dimension angulaire v. Cette dimension est connue par 3 estimations différentes. La première repose sur une comparaison avec la lune : elle ne peut fournir qu'un ordre de grandeur car elle ne permet pas au témoin de contrôler lui-même des déclarations. Nous ne retiendrons donc que les estimations ayant eu un support graphique soit ₂ = 4,6° et ₃ = 5,2° ( chap. 3 §6.1. ).

La distance Dv est fonction de la valeur de L choisie : le tableau 2 retient la longueur la plus probable ainsi que ses bornes de validité.

TABLEAU 2 : Distance Dv ( en m ) en fonction de L

LONGUEUR

ESTIMATION CRITERE DATE ANGLE Lmin
4,3 L
5,5 Lmax
7,2

1 Arbre 1979 4,6° 53 69 90

2 Test 1981 5,2° 47 61 79

MOYENNE 4,9° 50 65 85

Discussion :

L'utilisation des angles ₂ et ₃ conduit à une distance Dv qui pourrait varier du simple au double entre 47 et 90 m, la valeur la plus probable étant 65 m. Là encore, il convient de tenter une évaluation de la marge d'erreur. L'objet a été vu en l'air pendant peu de temps, ce qui rend difficile a priori une bonne observation de sa dimension angulaire, mais à une altitude faible ce qui a permis une comparaison avec les détails du paysage. Dans ces conditions, l'erreur sur _v pourrait ne pas excéder 30 % soit 3,77° < _v < 6,37° ( réf. _v = 4,9° ). Finalement, l'erreur sur Dv résulte du cumul des erreurs sur _s et _v et s'élève donc à près de 70 % :

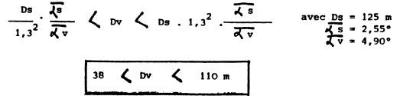
4.1.2. Altitude

Rosine a observé l'objet dans un plan horizontal ou un peu au dessus ( chap. 3 §4.1.a ). Le sol de la cuisine où elle était assise est à une altitude ( conventionnelle, cf. §2.4 ) de 11,5 m, ses yeux étaient par conséquent à 12 m environ. Le sommet des arbustes F au niveau desquels l'objet serait passé est a une altitude de 12,6 m ( site 0,64° ) tandis que sa base est à 8,7 m. Si la direction d'observation était effectivement horizontale, l'altitude de l'objet au dessus du sol supposé horizontal ( en réalité, il ne l'est pas mais peu importe ici ) serait donc de 3,3 m. Pour un site légèrement positif, l'altitude augmente en fonction de la distance : 0,1 m pour 10 m au site 0,6° par exemple ce qui correspond à une altitude par rapport au sol de 4 m à 70 m de P1.

Discussion :

Dans ces conditions de distance et d'altitude, une appréciation directe de l'une et de l'autre par le témoin est concevable. Malheureusement, Rosine n'a pas été spécifiquement interrogée sur ce point ( les enquêteurs ont conduit l'audition en supposant le phénomène éloigné ). On trouve, cependant, dans le P.V. de gendarmerie une indications initialement écartée comme subjective et sans valeur, qui prend un intérêt nouveau dans le présent contexte : "La chose volait à une hauteur de 2,50 m, environ" ( 2 déc. 79 ). En effet, si l'objet est proche, seule est en question l'aptitude du témoin à donner une expression numérique de l'altitude observée et non, comme dans le cas d'un objet éloigné, le principe même d'une telle évaluation. Il est difficile d'exprimer la marge d'erreur sur l'indication "2,5 m" mais en tout état de cause, on peut tenir pour bon l'accord entre la hauteur évaluée par Rosine et celle qui résulte du calcul.

4.2. La trajectoire calculée est-elle compatible avec les obstacles au sol ?

4.2.1. Position du problème

Une altitude d'évolution aussi basse que celle que nous venons de calculer est, au vrai, assez singulière. La zone survolée est truffée d'obstacles de hauteurs diverses : maisons, haies d'arbres ou d'arbustes, poteaux et pylônes, fils électriques et téléphoniques. Une nouvelle question se pose donc : est-il possible qu'un objet supposé solide ait pu survoler sans collision la zone considérée à l'altitude prescrite ?

4.2.2. Résolution

Pour opérer cette vérification dans les conditions les plus rigoureuses, il convient de considérer un segment de trajectoire suffisamment long. La trajectoire n'a pas été observée en tout point par Rosine, force est donc de l'extrapoler. Le plus simple est de la supposer rectiligne, passant par le point O et un point N contenu dans le plan de fin d'observation en vol et visible de P1 sous une faible hauteur angulaire.

Pour conserver toute sa généralité à la vérification, nous ne choisirons pas d'emblée une distance P₁N mais nous examinerons toute la plage des distances possibles pour savoir s'il existe au moins une distance susceptible de satisfaire les contraintes posées sur la trajectoire.

La première méthode qui vient à l'esprit pour résoudre ce problème, consiste à reconstituer des "coupes" du terrain et de ses obstacles dans une série de plans verticaux passant par O, chacun d'eux contenant la trajectoire imposée ON. Considérons par exemple, un de ces plans tel que P₁N = 60 m. On constate immédiatement que cette trajectoire est impossible car elle intersecte le pylône A3 ( il culmine à une altitude de 24,5 m ! ).

Cette méthode est parlante mais très fastidieuse. Le même résultat peut être obtenu d'une manière plus élégante et d'emblée générale, par le calcul.

Considérons, en effet, un sommet d'obstacle quelconque M et traçons la droite MO. Cette droite intersecte en un point N' le plan vertical V passant par P₁ et contenant la direction de fin d'observation en vol. A chaque point M est ainsi associé un point N' de telle sorte que l'ensemble des obstacles se trouve projeté sur le plan V. On obtient alors une sorte "d'ombre chinoise" : tous les points N de V situés dans "l'ombre" due aux obstacles correspondent évidemment à des trajectoires interdites, seuls les points N des zones "éclairées" indiquent des trajectoires autorisées.

Le résultat de cette projection des obstacles sur le plan V de fin d'observation en vol est montré sur la figure A3.4. Il est également résumé sous une forme plus schématique dans le tableau 3.

4.2.3. Discussion

Il s'agit maintenant, à l'aide des données de la figure A3.4 et du tableau 3, de distinguer les trajectoires autorisées et interdites. Nous considérerons qu'une trajectoire calculée est interdite lorsque le site sous lequel elle peut être observée à partir de P1 s'éloigne trop du site de la trajectoire observée par Rosine ( évaluée à 0,6° ). Mais comment exprimer l'écart entre la trajectoire observée et la trajectoire calculée ? Et comment fixer le seuil à partir duquel cet écart devient excessif ?

La réponse la plus adéquate à la première question consiste à exprimer comme précédemment l'écart sous forme d'une erreur relative S/So où S est la différence des sites observés et calculés. Rosine ayant dessiné l'objet au sommet de la haie, on peut prendre la hauteur angulaire de cette haie comme référence So, ce qui revient à admettre que le témoin est sensible à l'altitude de l'objet au dessus du sol. On prendra : So = 4,5°.

La seconde question est plus délicate car il faudrait entreprendre une expérimentation spécifique pour y répondre. En son absence, nous reprendrons la même incertitude que celle déjà utilisée sur _s et _v, soit 30 %.

FIGURE A3.4. : Projection des obstacles au sol sur le plan vertical V passant par la direction de fin d'observation de l'objet en vol.

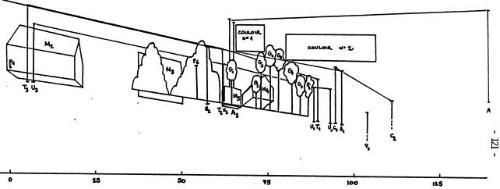
Cette projection fait correspondre à tout point M de l'espace un point M' de V, représenté sur cette figure, tel que M, M' et O soient alignés. Elle permet de déterminer les obstacles qui limitent, effectivement, les déplacements d'un objet parcourant une trajectoire rectiligne s'achevant en O. Seuls les couloirs n°1 et 2 sont compatibles avec le témoignage de Rosine.

TABLEAU 3 : TRAJECTOIRES INTERDITES PAR LES OBSTACLES AU SOL

Le plan vertical V ( passant par le point d'observation P1 et contenant la direction de fin d'observation en vol ) a été divisé en 11 intervalles dans la fourchette de distances possibles objet-témoin ( 38 - 110 m, § 4.1. ).

A l'exception du 5^ème ( pylône A3 ), ces intervalles ont même largeur ( 7,5 m ). Dans chacun d'eux, on a recherché le point N', intersection de la droite MO ( joignant le sommet M d'un obstacle quelconque à la trace O ) et du plan V, ayant l'altitude H la plus grande et qui, pour cette raison, correspond à la trajectoire la plus basse possible.

Le tableau indique l'attitude H ( niveau zéro au voisinage de O) du point N', la nature de l'obstacle M correspondant, la hauteur H du point N' au-dessus du plan horizontal passant par P1, le site S de N' vu de P1, l'erreur relative S/So qu'aurait commis le témoin si la trajectoire réelle avait été la plus basse possible dans chaque intervalle ( avec S : différence entre le site calculé S et le site d'observation évalué à 0,6° ; et So : hauteur angulaire de l'objet au-dessus du sol évaluée à 4,5° ).

Dans ces conditions, le tableau 3 montre que toutes les trajectoires situées à moins de 65 m, c'est-à-dire en deçà du pylône A3, sont interdites ( les lignes T et U séparées par 2 m seulement ne permettraient pas le passage de l'objet entre elles ) tandis que toutes les trajectoires situées au delà peuvent être considérées comme autorisées à l'exception de la zone 74 - 80 m.

En conclusion, il existe 2 couloirs, le premier entre 65 et 74 m, le second entre 80 et 110 m ( fig. A3.3 et A3.4 ) où un objet solide aurait pu passer sans entrer en collision avec les obstacles au sol et sans s'écarter de manière significative de la description fournie par Rosine. L'analyse précédente, si elle ne permet pas, bien entendu, de démontrer la présence d'un tel objet, ne permet pas non plus, comme on aurait pu le penser, de l'infirmer.

4.3. Synthèse : détermination du couloir le plus probable

Quelle est la conséquence de la restriction des trajectoires possibles aux 2 couloirs que nous venons de calculer sur les fourchettes de validité des dimensions angulaires _s et _v déduites du témoignage de Rosine ?

Figurons par un segment la fourchette Dv calculée précédemment à partir de Ds, _s, _v et d'hypothèses vraisemblables sur les erreurs relatives possibles sur ces angles. La prise en compte des obstacles fait apparaître des zones interdites comme suit :

Les valeurs Dv ont été calculées à partir de

_s et

_v par la relation :

Par conséquent, les restrictions sur Ds correspondent à des restrictions sur le rapport Ds / Dv égal au rapport _s / _v pour des angles suffisamment petits. Sachant que Ds = 125 m il vient :

Pour mieux apprécier la signification des rapports _s / _v interdits, dessinons un diagramme de _s en fonction de _v ( fig. A3.5 ). Chaque rapport _s / _v caractérise la pente d'une droite passant par l'origine. Seules les aires du plan compris entre les droites de pente 0,52 et 0,59 ainsi que 0,64 et 0,85 correspondent à des couples ( _s , _v ) autorisés. Il faut éliminer de plus, toutes les zones correspondant à des erreurs relatives sur _s ou _v supérieures à 30 %. Les deux aires résiduelles ainsi définies présentent des contours fort différents qui conduisent aux remarques suivantes :

(1) Si l'objet emprunte le couloir n°1 ( 65-74 m ), sa distance est très bien connue ( Dv = 70 m ). Par contre, les restrictions apportées par le diagramme aux couples ( _s , _v ) sont peu importantes si bien que l'incertitude sur sa longueur demeure grande ( 4,6-7,2 m au lieu de 4,3-7,2 m ). Cependant le point le plus important, si l'objet est passé par le couloir n°1, c'est que Rosine a correctement évalué le rapport _s / _v ( 0,56 calculé contre 0,52 témoigné). Par contre, l'erreur relative sur l'altitude est forte ( 26 %, tableau 3 ).

(2) Si l'objet emprunte le couloir n°2 ( 80-110 m ), sa distance est moins bien connue mais les restrictions apportées par le diagramme sont plus sévères si bien que ses longueurs autorisées se limitent à 5,3-7,2 m. Cela signifie que Rosine a plutôt sous-évalué la valeur de _s. De même, _v se trouve confirmé à l'intervalle 3,8-5,1° ce qui implique que Rosine a sur-évalué la valeur de _v. Il en résulte que si l'objet est passé par ce couloir, Rosine n'a pas correctement évalué ses dimensions relatives au sol et en vol ( 0,74 calculé en moyenne contre 0,52 témoigné ). Par contre, l'erreur relative sur l'altitude est nulle ( tableau 3 ).

Il apparait donc que le rapport _s / _v est un paramètre important à prendre en compte, au même titre que les angles _s et _v considérés isolément, et ce d'autant plus que le système perceptif humain est normalement mieux adapté au relevé des grandeurs relatives qu'à celui des grandeurs absolues. L'incertitude sur le rapport _s / _v pourrait donc être inférieure à celle sur _s et _v. Le fait que le couloir n°2 conduise à une erreur relative de 42 % sur ce rapport ( nettement supérieure au seuil des 30 % ), contre seulement 8 % pour le couloir n°1, incite à accorder une plus grande vraisemblance à cette dernière solution, même si elle est en partie compensée par l'erreur sur l'altitude.

Conclusion :

Les hypothèses faites, en ce qui concerne la trajectoire de l'objet ( rectiligne passant par O ) et les indications du témoin ( incertitude relative sur les valeurs angulaires et leur rapport n'excédant pas 30 % ), conduisent à considérer le couloir n°1 comme le plus probable. Au moment où Rosine cessait de l'observer, l'objet se trouvait donc à 70 m d'elle à une altitude conventionnelle de 14 m environ.

L'arbre G1, étant dans ce couloir ( fig. A3.3. ), on s'expliquerait ainsi pourquoi Rosine, dans ses dessins ( chap. 3, fig. 3.10 ), associe cet arbre à l'objet ( chap. 3, §6.1 ) : elle aurait eu l'impression d'une grande proximité entre les deux. Bien qu'elle ait été là encore incapable d'expliciter verbalement son impression, on peut légitimement y voir une confirmation des calculs précédents.

FIGURE A3.5 : Diagramme indiquant les dimensions angulaires autorisées pour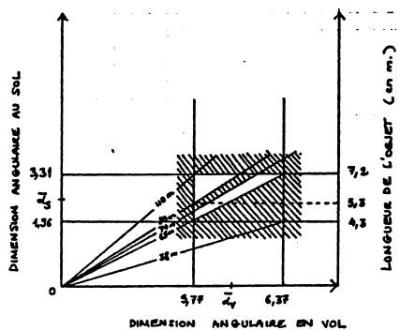

_s ( au sol ) et

_v ( en vol ).

Les restrictions proviennent :

de l'erreur relative sur ces angles évaluée au maximum à 30 % des valeurs moyennes retenues ( rectangle centré sur _s et _v ),
de la restriction des trajectoires possibles aux couloirs n°1 et n°2 en raison des obstacles au sol. Ces deux facteurs limitent les couples ( _s , _v ) possibles au quadrilatère non hachuré médian ( couloir n°1 ) et au triangle non hachuré supérieur ( couloir n°2 ).

4.4. Vitesse

Rosine a remarqué que "la chose ne volait pas tellement vite, toutefois, je ne puis dire à combien" ( P.V. 2 déc. 79 ). On sait que la durée d'observation en vol fut brève, de l'ordre de la seconde, mais la seule indication quantitative effectivement disponible est le temps qui s'est écoulé entre le moment de l'observation en vol et le début de l'observation au sol à la sortie du garage : 30 secondes ( chap. 3, §3.2. ).

La longueur de trajectoire observée a été évaluée à 5° environ ( chap. 3, §4.1. ) ce qui correspond à une distance de 6,5 m pour la trajectoire déterminée précédemment ( Dv = 70 m ). En prenant une durée d'observation de une seconde pour fixer les idées, l'objet aurait été animé d'une vitesse de 6,5 m/s ( 23 km/h ) et aurait parcouru les 94 m le séparant du point O en moins de 14 secondes, c'est-à-dire bien avant la sortie du témoin hors du garage.

5. - STRUCTURE DE L'OBJET

La description de l'objet en vol par Rosine s'accorde très difficilement avec celle d'un disque entouré de lumières ponctuelles sur sa périphérie car la direction d'observation était, rappelons le, peu différente de l'horizontale ( 1,6° pour la trajectoire retenue ). Elle s'accorde beaucoup mieux avec celle d'un objet dont la section longitudinale ( selon un plan vertical passant par la direction de déplacement aurait eu la forme décrite par le témoin et aurait porté une couronne unique de feux ponctuels alignés suivant un axe avant-arrière.

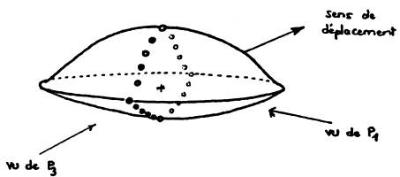
L'objet en vol a été observé par son côté droit. Au sol, si on admet qu'il n'a pas pivoté sur lui-même lors de l'atterrissage, il l'a été par l'arrière, ceci en raison de la position de P3 qui est peu éloigné de la trajectoire la plus probable. Deux conséquences s'en déduisent ( fig. A3.6 ) :

la forme observée ayant été à peu près la même en P1 et P3, l'objet présentait les mêmes sections longitudinalement ( vu de P1 ) et transversalement ( vu de P3 ). En généralisant, on peut admettre qu'il présentait une symétrie de révolution autour de l'axe médian vertical.
si les lumières ponctuelles étaient disposées uniquement suivant la section longitudinale, elles ne pouvaient plus, de P3, être observées sur le pourtour de la silhouette mais uniquement suivant une ligne approximativement médiane, à condition que ces feux aient rayonnés dans toutes les directions. On pourrait interpréter ainsi la contradiction apparente des propos de Rosine qui déclare d'une part, que "la chose posée avait toujours les lumières allumées" et d'autre part qu'elle n'a "rien vu de particulier sur le pourtour de l'engin" ( chap. 3, §5.2.1. ).

FIGURE A3.6 : Structure hypothétique de l'objet d'après la description de Rosine

6 - RECONSTITUTION

Le phénomène décrit le 27 novembre 1979 vers 17 H 15 par Rosine et secondairement par Lucille, ainsi que par d'autres témoins dont les déclarations n'ont pas été utilisées dans la présente étude, peut être tenu, à titre hypothétique, pour un objet solide. L'analyse conduite sur la base de cette hypothèse, permet de proposer une reconstitution du phénomène susceptible de rendre compte de manière cohérente de l'observation des témoins. Bien que ses divers éléments n'aient pas été établis aussi solidement les uns que les autres, il est utile pour conclure de considérer la reconstitution la plus vraisemblable pour elle-même, sous une forme volontairement schématique, sans référence aux données qui ont permis dé l'établir et allégée des discussions auxquelles elle donne lieu ( fig. A3.7 ).

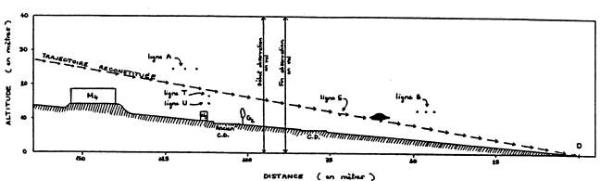
Un objet se déplaçant à une vitesse de l'ordre d'une vingtaine ou d'une trentaine de km/h a survolé à basse altitude sur une centaine de mètres au minimum une zone semi-rurale comportant des habitations, routes, haies, pylônes et poteaux. Il s'est faufilé entre ces obstacles suivant une trajectoire descendante supposée rectiligne, orientée NNO - SSE ( azimut 149° ) inclinée de 9,5° sur l'horizontale. Il est ainsi passé à 5 m au dessus d'une maison, à 5 m à droite d'un pylône puis à 5 m sous les câbles correspondant ( tension 63 kv ). Il a frôlé une ligne électrique située à 7,5 m du sol, le sommet d'un arbre de 6,5 m et, après avoir franchi une route, une ligne téléphonique à 6 m du sol. Il a ensuite survolé un champ de maïs récemment coupé ce qui l'a amené à passer à mi-distance entre une ligne électrique à moyenne tension et le sol. Enfin, il s'est immobilisé durant 2 minutes au moins au dessus d'une friche en forte déclivité située au bord du champ, où il a laissé dans l'herbe, une empreinte durable.

Cet objet était circulaire, d'un diamètre de l'ordre de 6 m et de 2 m de haut environ. Il émettait une luminosité d'ensemble s'apparentant à une phosphorescence, portait une douzaine de feux ponctuels alternativement rouges et blancs, alignés d'avant en arrière sur ses faces supérieures et inférieures, et produisait un son léger continu tant en vol qu'à l'arrêt.

Observé de plusieurs endroits différents, l'objet a été initialement découvert en vol, peu avant qu'il ne franchisse la route, par Rosine seule à travers la fenêtre de la pièce où elle se trouvait ( soit à une distance de 70 m dans une direction O/E, azimut 81°, faisant un angle de 69° avec la trajectoire ), puis immobile au sol, à partir de 30 secondes plus tard, le temps pour le témoin de sortir de chez elle. L'observation la plus nette de l'objet au sol, faite au temps t = 45 s, d'une distance de 125 m en direction SSE ( azimut 144° ), fait état à proximité immédiate de l'objet précédent d'un objet secondaire, également lumineux, de 1,5 - 1,8 m de haut, interprété comme un personnage. Rosine apeurée ayant été prévenir sa voisine Lucille, l'objet principal est encore perçu, 2 mn environ après sa découverte, d'une distance de 175 m en direction ESE ( azimut 102° ).

FIGURE A3.7 : Reconstitution de la trajectoire

La figure montre une coupe de terrain selon un plan vertical passant par la trajectoire la plus probable ( couloir n°1 ). La position et la hauteur des obstacles sont à l'échelle. La pente de la trajectoire ( 9,5° ) peut être comparée à l'inclinaison ( 11° ) de l'objet dessiné par Rosine ( chap. 3, fig. 3.10B ).

7 - CONCLUSIONS

(1) La question à laquelle j'ai tenté de répondre dans ce travail n'est pas, comme une lecture superficielle pourrait trop facilement le faire croire "QU'ONT DONC VU EN RÉALITÉ ROSINE ET LUCILLE LE SOIR DU 27 NOVEMBRE 1979 ?", question qui ne peut recevoir au mieux qu'une réponse prudente et provisoire, et au pire pas de réponse du tout. La question que je me suis posée est au contraire, la suivante : "COMMENT PEUT-ON CONNAITRE LE MIEUX POSSIBLE CE QUE LES TÉMOINS PRÉTENDENT AVOIR VÉCU ET JUSQU'A QUEL DEGRÉ DE PRÉCISION PEUT-ON ALLER DANS LA DESCRIPTION ET L'ANALYSE DU PHENOMENE ALLÉGUÉ ?" C'est notre aptitude à recueillir un vécu fugitif, à la quantifier, à construire sur lui un raisonnement, à en déduire une reconstruction théorique qui est en cause.

(2) De ce point de vue et en dépit d'insuffisances évidentes des témoignages, une analyse quantitative s'est avérée possible et a permis de mieux comprendre le cas. A la lumière de la reconstitution, certaines déclarations ou détails Indiqués par Rosine semblent prendre un intérêt qu'ils ne possédaient pas initialement et qui, s'ils avaient été connus lors des auditions auraient pu en modifier le cours. Ceci montre l'intérêt dans tous les cas, d'une réflexion approfondie, si possible quantitative, sur les données initialement recueillies de manière à corriger ses impressions premières et à préparer une seconde investigation dans les délais les plus brefs.

(3) L'étude effectuée, en chapitre 3 et Annexe 3 n'a pas mis en évidence d'incohérences manifestes dans le témoignage de Rosine, ou d'impossibilités physiques patentes. La méthode quantitative utilisée se prêtait pourtant à leur mise en évidence par la comparaison d'aspects a priori distincts : tailles angulaires et distances, hauteurs angulaires et obstacles, durée et vitesse. Les indications fournies par Rosine, en dépit de leurs insuffisances et de leurs imprécisions sur de nombreux points, présentent donc une remarquable cohérence tant interne qu'externe.

(4) Si le présent cas n'est exceptionnel ni par la qualité des observateurs, ni par la qualité et la quantité des informations qu'ils ont fournies, la cohérence d'ensemble de l'observation de Rosine, la présence de témoins en 2 ( peut-être 3 ) endroits distincts et l'existence d'une empreinte sur le sol apparemment liée au phénomène, lui confèrent un indéniable intérêt. Or, on ne peut qu'être frappé au passage par la facilité avec laquelle toutes les informations recueillies sur cet événement auraient pu ne jamais parvenir à notre connaissance. Tout repose en définitive sur la vision très brève d'un phénomène insolite par Rosine et sur sa panique ultérieure sans laquelle la gendarmerie n'aurait jamais été prévenue, les traces n'auraient pas été recherchées non plus que les autres témoins ( puisque nous n'avons eu connaissance de leur existence qu'un an plus tard ). Il semble donc que la rareté de semblables occurrences tienne d'une part à la faible probabilité d'une observation suivie de rapport et d'autre part, lorsqu'elle sont rapportées, à la modicité des efforts accomplis à ce jour pour collecter toutes les informations disponibles.

(5) Il est clair également qu'il est possible d'aller beaucoup plus loin dans l'étude des témoignages qu'on ne le pense généralement, plus loin en particulier qu'il n'a été possible de le faire dans cette étude. Ses principales faiblesses résultent d'une utilisation trop tardive des tests d'évaluation des données angulaires et de la fixation un peu arbitraire des marges d'erreurs à 15 % pour les longueurs ayant pu être comparées simultanément dans de bonnes conditions, 30 % dans tous les autres cas. Ces valeurs sont à rapprocher de la différence de 40 % entre 2 silhouettes successives du test de détermination des dimensions angulaires ( voir chap. 3, figure 3.13 ). J'ai supposé qu'un tel écart introduirait une différence sans ambiguïté entre deux silhouettes successives. Bien entendu, ces valeurs sont utilisées ici à titre de première approche, et faute de mieux, car il est évident que les erreurs relatives dépendent en réalité du témoin, des grandeurs à évaluer et des conditions d'observation. Quoi qu'il en soit, ces méthodes sont susceptibles d'être améliorées et rendues reproductibles, c'est-à-dire progressivement dégagées des particularités liées à tel ou tel témoin, à telle ou telle condition expérimentale ou à telle ou telle description phénoménale.

(6) Enfin, il est plus manifeste encore à la suite de ce travail que l'investigation approfondie d'un cas complexe comme celui-ci est un travail de longue haleine faisant appel à des techniques très diverses ( de l'audition du témoin à l'analyse des échantillons recueillie sur les traces ) qui supposent toutes des mises au point et des analyses longues et difficiles. Les progrès seront donc nécessairement lents. Ils devraient cependant permettre une utilisation de plus en plus féconde des meilleurs cas, ceux où il y a conjonction de phénomènes se prêtant à l'analyse physique et de bonnes observations ; cas, certes rares, mais qui sont restés à ce jour trop souvent ignorés ou inutilisés faute d'une investigation appropriée.

SUITE...

CENTRE NATIONAL D'ETUDES SPATIALES

NOTE TECHNIQUE N° 8

Enquête GEPAN n° 79/06

Table des matières

ANNEXE 3

RECONSTITUTION DU PHÉNOMÉNE FONDEE SUR L'HYPOTHÈSE D'UN OBJET PHYSIQUE UNIQUE

RECONSTITUTION DU PHENOMENE FONDÉE SUR L'HYPOTHÈSE D'UN OBJET PHYSIQUE UNIQUE

1 - INTRODUCTION

2 - METHODES

3 - L'OBJET A L'ARRET : POSITION ET DIMENSION

4 - L'OBJET EN VOL : TRAJECTOIRE ET VITESSE

5. - STRUCTURE DE L'OBJET

6 - RECONSTITUTION

7 - CONCLUSIONS

NOTE TECHNIQUE
N° 8