CENTRE NATIONAL D'ETUDES SPATIALES

Groupe d'Etudes des Phénomènes Aérospatiaux Non-identifiés

Toulouse, le 27 avril 1981
N° 110 CT/GEPAN


 

NOTE TECHNIQUE N°3


 

METHODOLOGIE D'UN PROBLEME
Principes & Applications

(Méthodologie - Isocélie - Information)

TABLE DES MATIÈRES

PRÉSENTATION

1 - LE PROBLÈME DES PHÉNOMÈNES AÉROSPATIAUX NON IDENTIFIÉS

1.1. Introduction
1.2. Quelques idées fausses
1.3. Quelques études contradictoires
1.4. Que faire ?

2 - ÉLÉMENTS D'UNE MÉTHODOLOGIE DE RECHERCHE

2.1. Remarques préliminaires
2.2. Schéma directeur
2.3. Stratégie de recherche
2.4. Conclusion

3 - ÉTUDE DE L'ISOCÉLIE

3.1. Les résultats de JC. FUMOUX et JF. GILLE
3.2. D'autres résultats
3.3. Remarques méthodologiques

4 - QUESTIONS D'INFORMATION

4.1. Questions de principes
4.2. Quelques aspects pratiques
4.3. Polémique de la recherche et recherche de la polémique
4.4. A propos des erreurs de lecture

5 - CONCLUSION DES CHAPITRES PRÉCÉDENTS

 

 

CHAPITRE III

- ETUDE DE L'ISOCÉLIE -

P. BESSE

 

La Dépêche du Midi
Mercredi 12 décembre 79

 

INTRODUCTION *

(*) Dans tout ce chapitre, les références sont citées en indiquant les 3 premières lettres de l'auteur et la date de parution ( cf. Bibliographie ).

Ayant étudié la "vague" de 1954, Aimé MICHEL ( MIC 58 ) affirma que les lieux d'observations ne se répartissaient pas au hasard sur la surface du globe, mais suivant des alignements. Ceci engendra tout un lot de critiques plus ou moins justifiées ( TOU 70, VAL 66, SAU 72, ... voir la bibliographie ) qui amenèrent à rejeter cette hypothèse ( appelée orthoténie ) au bénéfice de celle d'une distribution compatible avec les lois du hasard.

Plus récemment, ( cf. FUM 78 ), ce type d'approche reparaît sous le nom d' "isocélie" : il s'agit de savoir si les "quasi-atterrissages d'OVNI" obéissent à une "logique de triangulation". Des calculs furent développés ( cf. GIL 80 ) et leur conclusion présentée le 11 décembre 1979 à PARIS, lors d'une conférence de presse ( cf. Le Monde du vendredi 14 décembre 1979, p. 29 ). Cette démarche publicitaire fut organisée par M. SCHNEIDER, Président du groupement privé CNROVNI ( Commission Nationale de Recherche sur les OVNI ) et obtint un certain retentissement dans les revues ufologiques, les journaux nationaux ou régionaux, et même certaines publications scientifiques...

Le présent travail se propose de reprendre les aspects techniques de "l'isocélie" afin de souligner les difficultés rencontrées dans ce type de démarche, et les diverses erreurs commises dans l'étude de MM. FUMOUX et GILLE.

 

3.1. LES RÉSULTATS DE JC. FUMOUX ET DE JF. GILLE

Ce paragraphe présente brièvement la démarche et les résultats décrits dans un document peu diffusé ( GIL 30 ).

3.1.1. PRÉLIMINAIRES

En situant les lieux "d'atterrissages" allégués de la "vague" de 1954 sur une carte, JC. FUMOUX remarque parmi tous les triangles définissables par les points, certains étaient isocèles. L'idée fut alors de chercher si le nombre de triangles isocèles formés par les lieux d'observations pouvait être imputé au seul hasard ou si un hypothétique facteur déterministe intervenait.

Pour cela, JF. GILLE compare les résultats en situation réelle avec ceux obtenus pour des simulations ou tirages aléatoires de points distribués uniformément. Quelques définitions sont nécessaires :

  • distance :
    La Terre est considérée comme étant une sphère de rayon R, R = 6366,1977 km ; La distance séparant deux points repérés par leur longitude et leur latitude, est la longueur de l'arc de grand cercle passant par ceux-ci.

  • triangle isocèle :
    Un triangle est considéré comme isocèle si la différence entre les longueurs de deux de ses côtés ( = distance entre les sommets ) est inférieure à une valeur fixée à l'avance : d.
    Pour les exemples traités, d = 2,5 km.

  • points rapprochés :
    ( voir Annexe 3, une discussion géométrique à ce sujet )
    Lorsque dans l'échantillon, deux points sont très rapprochés, ils constituent avec la plupart des autres points des triangles isocèles. Trois possibilités seront utilisées par le GEPAN :

    1. conserver ces points & compter tous les triangles isocèles,
    2. remplacer ces points par d'autres lieux d'observation suffisamment distants des autres ( ou par d'autres tirages aléatoires dans le cas d'une simulation ),
    3. laisser ces points mais ne pas prendre en compte les triangles isocèles dont un côté au moins est de longueur inférieure à une valeur donnée ( D = 10 km).

 

3.1.2. "CAS REELS"

Deux des échantillons ( notés JCF et JJV ) de cas d'observations "d'objets près du sol", utilisés pour l'étude, sont répertoriés en ( FIG 79 ). Il s'agit semble-t-il des mêmes 76 cas ; les coordonnées étant extraites de ( VAL 66 ) ( échantillon JJV ) et certaines étant relevées ou corrigées par JC. FUMOUX ou JF. GILLE ( GIL 80, échantillon JCF ). La liste est donnée en ann. 1. La numérotation est l'ordre chronologique de ( FIG 79 ).

 

3.1.3. SIMULATION

Pour simuler une distribution uniforme de points sur la France, en représentation sphérique, la démarche utilisée en ( GIL 80 ) est la suivante :

  • tirage aléatoire de points sur un rectangle,

  • ne sont retenus que les points appartenant a un tronc de cône développé qui est le cône de projection LAMBERT de la carte de France,

  • passage des coordonnées LAMBERT aux coordonnées polaires,

  • élimination des points situés à l'extérieur du contour schématisé de la France ( FVAL, cf. figure 1 ) utilisé en ( VAL 66 ) pour simuler l'orthoténie. ( Voir figure 1, page suivante ),

  • élimination des triangles dont un côté est inférieur à 10 km opérée en ( GIL 80 ). Les résultats du GEPAN ( cf. 2.2.3 ) sembleraient montrer que cette opération n'a pas été effectuée par M. GILLE.

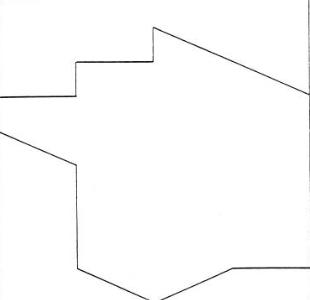
FIGURE N° 1 - Contour FVAL

La représentation est celle du plan ( longitude, latitude ), elle est très déformée. Ceci ne joue pas sur les résultats qui sont calculés en géométrie sphérique.

 

3.1.4. RESULTATS PRESENTES EN (GIL 80)

Le repérage des lieux est fait au millième de degré près ( #100 m ).
Ceci est négligeable par rapport aux inexactitudes dues à l'utilisation d'une carte en projection LAMBERT & à l'approximation de la Terre par une sphère au l ieu de l'ellipsoïde international. on suppose alors que ces erreurs sont majorées dans le cas "réel", comme dans le cas des simulations, par la différence ( d = 2,5 km ) admise entre les longueurs des côtés "égaux" des triangles isocèles.

Lorsque 76 points sont considérés, les nombres de triangles isocèles trouvés en ( GIL 80 ) sont les suivants :

Echantillon   JCF *    1776
Échantillon JJV * 1844
Echantillon JFG 1877
Simulation 1 1621
Simulation 2 1637
Simulation 3 1613
Simulation 4 1631

m = 1625.5
s = 10,63
(s désigne la moyenne, et m l'écart-type empirique calculé à partir des tirages effectués ( ici 4 ).

* : Il apparait qu'une confusion se soit glissée en ( GIL 80 ) pour l'appellation des échantillons JCF et JJV. JJV désigne ici la liste comportant certaines erreurs de ( VAL 66 ) et corrigées, semble-t-il dans la liste JCF. JFG désigne une sélection spécifique de ( GIL 80 ).

Si on suppose que la variable aléatoire X ( = nombre de triangles isocèles déterminés par 76 points uniformément distribués dans le contour FVAL ) est normale (N (m,s)), alors la probabilité de trouver un nombre de triangles isocèles supérieur ou égal à 1776 est :

L'événement considéré parait, au vu de ces résultats, très peu probable donc difficilement attribuable au seul hasard.

 

3.2. RÉSULTATS OBTENUS PAR LE GEPAN

La démarche employée maintenant est tout à fait similaire à celle décrite ci-dessus. Les différences et compléments proviennent avant tout de la nécessité d'évaluer l'influence des paramètres de la simulation.

 

3.2.1. SIMULATIONS ELEMENTAIRES

3.2.1.1. Mode opératoire

Un nombre NP de points sont tirs au hasard selon une distribution uniforme sur le carré [ 0,1 ] x [ 0,1 ]. Parmi tous les C3Np triangles possibles, les triangles isocèles ( à l'erreur admise d près ), sont dénombrés. Chaque simulation fournit ainsi un certain nombre X ( Np, d ) de triangles isocèles. Plusieurs simulations utilisant les mêmes paramètres ( Np, d ) conduisent à une estimation m du nombre moyen théorique M de triangles isocèles. Ces simulations élémentaires demandant peu de temps de calcul, elles peuvent être répétées pour différentes valeurs des paramètres.

3.2.1.2. Nbre de points (NP )

Le tableau ci-dessous donne les résultats moyens sur 10 tirages de NP points sur le carré [ 0,1 ] x [ 0,1 ] :

d = 0.0030

  NP     10     20     30     40     50     60     70     80     90     100 
m   3,3        25.6       88.4       223,2      422.8      736,4      1215.4     1820,1     2620,9     3602.5  

Si on considére que le carré a la superficie de la France continentale ( # 542 800 km2 ), la longueur des côtés est donc de 736,75 km et l'erreur admise ( d ) représente alors à l'échelle une distance de :

Le nombre moyen de triangles isocèles est une fonction sensiblement exponentielle du nombre de points tirés ( cf. figure n° 2 ).

 

 

 

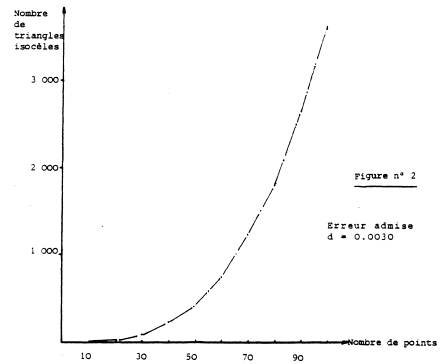
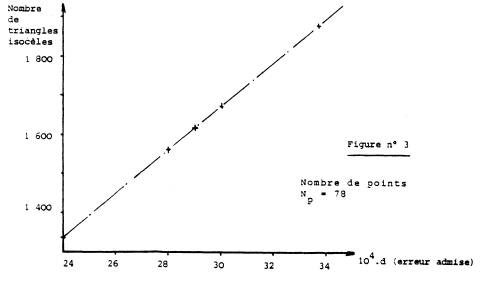
3.2.1.3. Erreur admise (d)

Le nombre de points tirés ( NP ) est cette fois fixé à 78 ( * ) et l'erreur admise varie. La moyenne est calculée à partir de 100 tirages successifs.

  d    de (en km)    m  
  0,0024    1,77  1337,88 
  0,0028    2,06  1561,17 
  0,0029    2,14  1616,17
  0,0030  2,21  1671,75
  0.00337  2,48  1878

NP = 78

(*) Comme pour les premiers résultats de ( FUM 78 ).
Pour permettre la comparaison avec ceux de ( GIL 80 ), les simulations suivantes utilisent 76 points.

La figure n° 3 montre que, pour la zone considérée, la variation de m est linéaire en fonction de l'erreur admise. A l'échelle, un accroissement de l'ordre de 100 mètres sur d, augmente approximativement de 76 le nombre moyen de triangles isocèles.

3.2.1.4. Distribution de X

Le nombre important de tirages ( 100 ) permet certainement une bonne estimation de la moyenne mais celle-ci doit être précisée par un intervalle de confiance qui nécessite la connaissance de la loi de probabilité de la variable aléatoire : X = "nombre de triangles isocèles".

Une simulation de 100 tirages de 76 Points fournit l'histogramme suivant ( d = 0,00337 ).

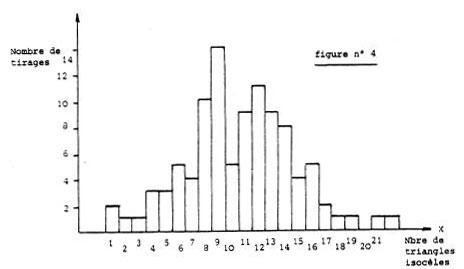
Le test d'ajustement ( ou test du X2 ), calculé en regroupant les classes ( 1 à 4 ), ( 5, 6 ), ( 16, 17 ) et ( 18 à 22 ), conduit à l'acceptation de l'hypothèse HO : la variable X suit une loi normale N ( m,s ), (le X2 est de 7,74 alors que, pour 9 degrés de liberté, la borne à 5 % est 16,92).

Sous l'hypothèse gaussienne ainsi acceptée, il est possible de calculer pour m et s, des intervalles de confiance bilatéraux. Si M et S désignent les paramètres théoriques de la loi de probabilité que l'on cherche à estimer ( cf. SAP 78 ) :

(1-alpha) est le niveau de confiance ou probabilité pour que l'intervalle contienne la valeur M.

s est l'estimation de l'écart-type, n le nombre de tirages, m l'estimation de la moyenne et t1- alpha/2 , qui dépend du nombre de degrés de liberté ( n-1 ) et du niveau de confiance 1- alpha , est donné dans la table des fractiles de la loi de Student. Et, de même :

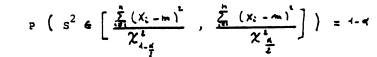
dépendent du nombre de degrés de liberté ( n-1 ) et du niveau de confiance ( 1- alpha ), ils se trouvent dans la table des fractiles de la loi du X2.

En résumé, l'hypothèse que la variable aléatoire X ( nombre de triangles isocèles ) est gaussienne, est légitime. Il est alors possible de calculer des intervalles de confiance pour encadrer la moyenne et l'écart type de la loi cherchée.

L'estimation m de la moyenne croit très vite avec le nombre NP de points considérés et est aussi très sensible aux variations de l'erreur admise d.

Il reste encore à évaluer l'influence de la forme du contour ainsi que celle de la procédure d'élimination des points trop rapprochés.

3.2.2. SIMULATIONS DETAILLEES

3.2.2.1. Mode opératoire

Afin de tenir compte de l'éventuelle influence de la forme du contour ou de celle de la rotondité de la Terre, et pour obtenir des résultats comparables à ceux de ( GIL 80 ), les simulations ont été calculées avec un modèle présentant un même niveau de complexité.

Ceci demande encore une fois ( cf. § 1.3. ), de simuler une distribution uniforme de points sur la France en représentation sphérique.

La démarche utilisée a été simplifiée :

  • Tirages aléatoires de points dans un rectangle limité d'un côté par un arc de cosinus :

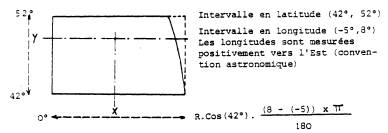
    L'ordonnée Y du point représente sa latitude, l'abscisse X sa position sur la portion d'arc du "parallèle Y". On obtient ainsi, représentés par leur latitude et leur longitude, une distribution uniforme de points sur la portion de sphère contenant la France.

    Cette procédure simplifiés évite, et est plus précise que le passage intermédiaire en coordonnées LAMBERT de ( GIL 80 ), tout en n'introduisant que des variations négligeables au niveau des comparaisons.

  • Les points à l'extérieur d'un contour donné sont ensuite éliminés. Deux formes sont utilisées : d'une part FVAL ( cf. figure n° 1) utilisée en ( GIL 80 ) et d'autre part FCNES ( cf. figure n° 5) extrait du "fichier continent" utilisé par le CNES ( chaque point de ce contour est précis à un kilomètre près )

  • Selon la procédure de traitement des points rapprochés choisie, élimination ou non de certains points et retirage éventuel de points complémentaires.

  • Les calculs sont refaits avec un tirage aléatoire de 76 points sur un carré normalisé à la surface de la France continentale.

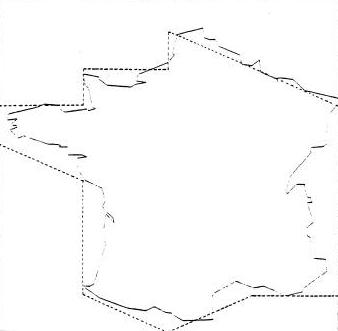
FIGURE N° 5

contour FCNES (en trait plein),
contour FVAL (en pointillé)

3.2.2.2. Résultats

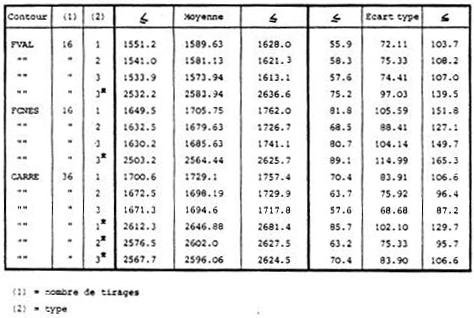
Les valeurs moyennes sont encadrées par un intervalle de confiance au seuil 95 % et 90 % pour les écarts-types ( en supposant que la distribution reste gaussienne, indépendamment de la forme du contour ).

Le type désigne la procédure de traitement des points trop rapprochés :

  • 1, 2, 3 : cf. § 1.1.
  • * : l'erreur admise (d = 2,5 km) est remplacée par une erreur relative admise de 1 %.

 

En utilisant les échantillons JJV et JCF contenant les cas "d'atterrissages" à la place de simulations, on trouve les résultats suivants :

TYPE JCF JJV
  1   1772 1840
  3     1612     1682  
  3*   2553 2620

En complétant JJV selon 1a procédure 2 avec des points supplémentaires ( cf. annexe ) après élimination des points trop rapprochés, on obtient 1693 triangles isocèles ( ** ).

(**) la liste de l'échantillon JFG utilisé également en ( GIL 80 ) nous ayant été communiqué qu'à la fin du travail, les résultats le concernant sont reportés en annexe.

3.2.2.3. Remarques

  • 1ère remarque :
    On note I (...) l'intervalle de confiance de la moyenne m (...) relatif à une simulation. Alors :

    Les raisons de ces inclusions ou disjonctions, sont claires :

    • la forme du contour joue un rôle mineur sur m ( cf. m ( CARRE ) - m ( FCNES ) de l'ordre de 20 unités ) qui parait croître avec la régularité du contour ( m ( FCNES 3* ) < m ( FVAL 3* )  < m ( CARRE 3* ) ) ;
    • par contre la surface delta délimitée par le contour joue un rôle déterminant :
      comme delta ( FVAL ) > delta ( FCNES ) ( voir figures 1 et 5 ), on trouve M ( FVAL ) < M ( FCNES ) et la différence est de l'ordre de 100 unités. Ceci s'explique simplement par le fait que l"'erreur admise" ( d ) est une erreur absolue. Ainsi, par homothétie, utiliser une surface plus grande revient à utiliser, à surface égale, une "erreur admise" plus faible. Comme ceci a été vu au § 2.1.3., le nombre m étant très sensible aux variations de l'erreur ( d ), il est ainsi très sensible aux variations de la surface.

    Ce résultat est alors confirmé par le fait que l'utilisation d'une "erreur admise relative" annule cette influence de la surface sur les résultats.

  • 2ème remarque :
    L'écart-type est lui aussi sensible à la forme et à la surface. De façon assez logique, il décroît avec la régularité du contour.

  • 3ème remarque :
    D'une manière triviale, le type 1 ( aucune élimination ) conduit à des résultats supérieurs ( de l'ordre de 30 unités ) aux autres types qui eux sont peu différenciés. Il parait raisonnable de penser que dans ( GIL 80 ) aucune élimination n'intervient** ( type 1 ) : seule I ( FVAL 1 ) contient la moyenne trouvée ( 1625,5, cf. § 1.4. ) et les résultats obtenus avec les échantillons JCF et JJV ne correspondent, à quelques unités près, qu'à ce cas.

** : Cependant, le programme décrit en ( GIL 80 ) suggère que l'élimination selon la procédure 3 serait utilisée en simulation.

3.2.2.4. Probabilités d'occurence

Relativement au contour FCNES, et pour chaque type de simulation on calcule la probabilité pour que la variable aléatoire X ( supposée gaussienne ) soit supérieure aux valeurs trouvées pour les échantillons JJV et JCF. Ceci conduit au tableau suivant :

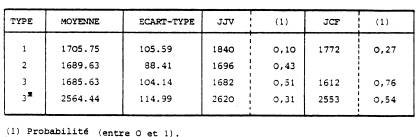
Conclusion :

Quel que soit le type de simulation et l'échantillon de "quasi- atterrissages" considéré, le hasard seul suffit à expliquer les résultats 'trouvés.

 

3.3. REMARQUES MÉTHODOLOGIQUES

Au-delà de la conclusion du paragraphe précédent, qui est le rejet de "l'hypothèse isocélique", il est possible de cerner les difficultés que comporte ce genre d'étude et donc les précautions à prendre.

3.3.1. DIFFICULTÉS

3.3.1.1. échantillonnage

Peu d'indications sont fournies en ( FUM 79 ) sur la façon dont a été faite la sélection des cas. Il est banal mais toujours nécessaire de rappeler que celle-ci doit être exhaustive ( tous les cas ) ou aléatoire ( échantillon statistique ) afin de conduire à des résultats valides. Les procédures de sélection ou d'élimination doivent être clairement explicitées afin d'évaluer les biais introduits.

3.3.1.2. Nature des distributions spatiales

Entre m ( FCNES 1 ) et m ( FCNES 3 ), la différence est de 20 unités. Pour l'échantillon JCF ( resp. JJV. ) la différence entre le type 1 et le type 3 est de 158 ( resp. 160 ) unités. Ceci conduit à penser que la simulation d'une distribution uniforme de points produit moins de couples de points très rapprochés ( < 10 km ) que n'en contiennent les échantillons "réels". En effet, comme il l'a déjà été souvent signalé ( BES 80 et bibliographie ), les lieux d'observations ne sont pas distribués uniformément mais de façon plus ou moins agrégative.

L'utilisation d'une distribution uniforme ( facile à simuler ) introduit un biais qui est en partie levé par l'élimination des points trop proches ( type 2 ) ou par celle des triangles dont un côté est trop court ( type 3 ). Les échantillons deviennent ainsi comparables.

3.3.1.3. Précision du modèle

La précision ou la validité des résultats obtenus (moyenne, écart-type) dépendent encore de deux facteurs :

  • le nombre de simulations influence directement la taille des intervalles de confiance ( cf. § 2.1.4. ) ;

  • la connaissance de l'influence des paramètres de la simulation permet "au mieux" d'affiner le modèle. Ainsi, dans le sujet traité le facteur important n'est pas le choix de la représentation ( plane ou sphérique ) mais bien dans une faible mesure ( 20 unités ) la forme du contour et surtout ( 100 unités ) la surface qu'il détermine.

3.3.2. ERREURS QUI CONDUISENT A L' ISOCELIE

La comparaison des résultats obtenus dans ce travail avec ceux présentés en ( GIL 80 ) met en évidence trois lacunes à l'origine des conclusions erronées :

  • problème lié aux points trop rapproches et à l'inadéquation des distributions spatiales entre les simulations et la "réalité" ( cf. § 3.1.2. ). Les résultats des simulations ( type 1 ) sont biaisées ( sous-évaluées ) par rapport à la réalité ( cf. Annexe 3 ) ;

  • le nombre insuffisant de simulations ( 4 ) concourt à une mauvaise estimation de l'écart-type : s = 10,6 alors que 1a simulation ( FVAL 1 ) montre que la probabilité :
    P (S > 55.9) = 0, 95

  • Enfin surtout, par rapport à la situation réelle, l'utilisation et du contour FVAL à la forme régulière et la superficie trop grande, faussent complètement les résultats.

3.3.3. CONCLUSION

Même en considérant des points rapprochés ( type 1 ) dans l'échantillon de "quasi-atterrissages", les résultats ne sont pas statistiquement significatifs ( 10 % - cf. § 2.2.4 ), et à plus forte raison en éliminant ces points ( type 2 ou 3 ).

Il faut donc l'accumulation des erreurs décrites ci-dessus pour que les probabilités d'occurence prennent des valeurs significatives ( cf. § 1.4 ).

Ce travail concerne exclusivement certains aspects techniques ( statistiques ) de l'isocélie ; il ne fait pas le tour des problèmes ; deux points particuliers n'ont pas été développés :

  • vérification des cas d'observations rapprochées et de leurs coordonnées,

  • intérêt de ce style de démarche.

A priori, la situation de 76 points d'observation est unique en tant que telle. Il est donc fort probable, en cherchant bien, de trouver une forme ou une figure géométrique ( cercle, carré, ..., polygones ) dont l'occurence parmi les 76 points "choisis" ne pourrait être réduite en théorie au seul hasard. Mais, quelle serait alors la valeur opérationnelle de telles hypothèses de travail, de telles recherches ?

Explicitement, les auteurs essayent de mettre en évidence une "logique" interne à la localisation des observations, donc, indépendamment des facteurs pouvant intervenir ( densité de population, localisation des enquêteurs, phénomènes de rumeurs, ... ), indépendamment du tétraèdre des observables décrit au Chapitre II.

Implicitement, ils prennent pour réalité objective ce qui n'en est qu'un reflet partiel et complexe, et essaient d'en révéler la signification intrinsèque. Cette motivation donne donc à ce type de travail, une connotation mystique*, l'excluant du cadre restreint d'une démarche scientifique. Il ne s'agit pas, bien sûr, d'opposer les épythètes "mystiques" et "scientifiques", car l'un s'applique à un objectif et l'autre à une démarche. Et, on se pose seulement la question suivante : une démarche scientifique doit-elle prétendre à révéler le "sens caché des choses" ?

(*) Au sens propre et non péjoratif ( : "recherche de signification cachée" )

 

ANNEXE 1

ÉCHANTILLONS

 

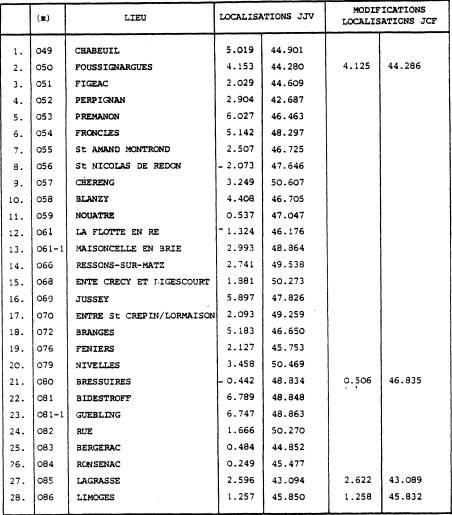
(*) Ordre chronologique FIG 79

Les longitudes sont comptées positivement vers l'Est (convention astronomique).

 

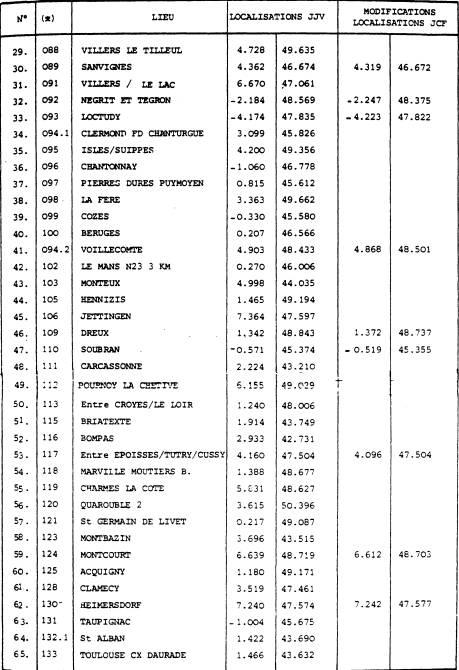
(*) ordre chronologique FIG 79

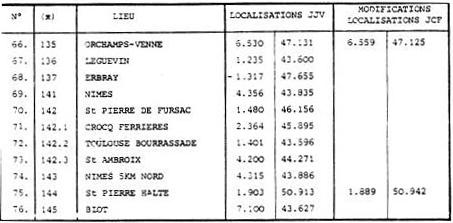
(*) Ordre chronologique FIG 79

Les coordonnées n'ont été ni vérifiées, ni modifiées.
Elles sont reproduites comme nous les a communiquées M. JC. FUMOUX, que nous remercions ici.

 

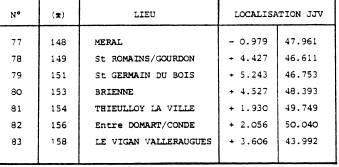
LISTE COMPLÉMENTAIRE (pour procédure type 2)

(*) Ordre chronologique FIG 79

 

ANNEXE 2

RÉSULTATS CONCERNANT L'ÉCHANTILLON JFG

Les longitudes sont comptées positivement vers l'Est (convention astronomique)

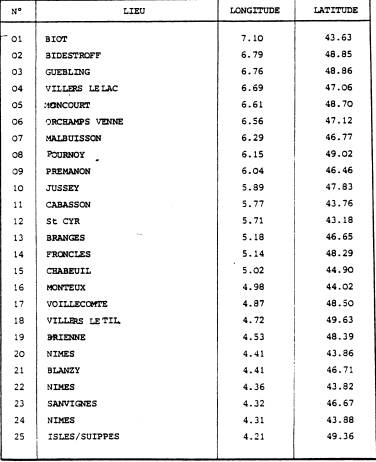
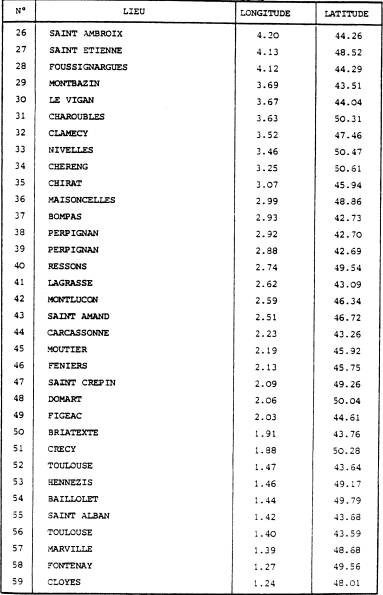
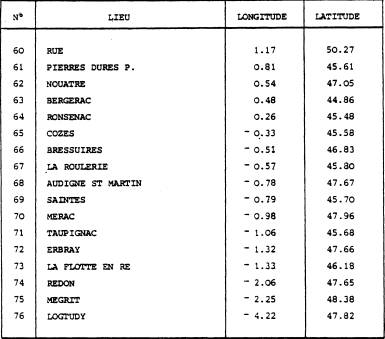
Les résultats trouvés à partir de l'échantillon JFG ne changent en rien les conclusions précédemment énoncées :

  • résultat de (GIL 80) : 1877

  • résultats trouvés :

    • type 1 (sans élimination) : 1829
    • type 3 (avec élimination des triangles dont un côté est < à 10 km ) : 1600

REMARQUES :

  • Alors que pour les échantillons JJV et JCF, les résultats retrouvés sont sensiblement les mêmes que ceux annoncés ( à quelques unités près cf. § 2.2.2 ), la différence est dans ce cas plus marquée.

  • La différence entre les types 1 et 3 est encore plus importante ( 229 unités ) que pour les autres échantillons. Ceci est normal car il comporte plus de groupes de points rapprochés ( par exemple : 3 observations près de Toulouse, 3 près de Nîmes, 2 près de Perpignan ).
    A l'examen, la liste JFG a été obtenue à partir de JJV et JCF en y substituant quelques points. En particulier, ont ainsi été rajoutés, un point près de Nîmes et un près de Perpignan, ce qui augmente l'aspect agrégatif et par conséquent, accroît artificiellement le nombre de triangles isocèles.

 

ANNEXE 3

INFLUENCE DE L'AGRÉGATION DES POINTS
SUR LE NOMBRE DE TRIANGLES ISOCÈLES :
INTERPRÉTATION GÉOMÉTRIQUE

Soient deux points A et B à la distance AB. Soit d l'incertitude admise sur l'égalité des côtés des triangles isocèles. A et B seront la base d'un triangle isocèle formé avec tout point extérieur aux branches de l'hyperbole ayant pour foyers A et B, et de distance aux sommets d ( l'hyperbole est le lieu des points dont la différence des distances à deux points fixes est constante ).

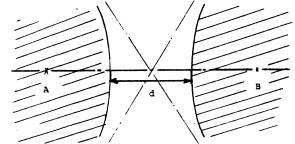La zone hachurée est le lieu des points qui ne forment pas avec A et B des triangles isocèles de base AB.

Si la distance AB est petite, les branches de l'hyperbole s'aplatissent sur AB. Il y a de plus en plus de points qui forment avec AB, des triangles isocèles de base AB.

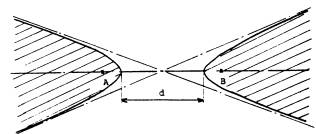
Si AB est très proche de d, presque tous les autres points formeront avec A et B, des triangles isocèles de base AB.

Si AB est inférieur ou égal à d l'hyperbole disparaît et tous les autres points forment, avec A et B, des triangles isocèles de base AB.

Pour un jeu de quelques 76 points, nous avons vu que chaque point participe en moyenne à 20 à 25 triangles isocèles. Si B est proche de A, il participera à peu près à autant de triangles isocèles que A ( si B n'existait pas ) et la plupart du temps avec les mêmes autres couples de points ( soit de 20 à 25 triangles ). Mais, de plus, AB formeront la base de triangles isocèles en les associant avec la plupart des autres points. On peut faire ainsi apparaître quelques 70 triangles isocèles simplement en introduisant dans l'échantillon un point proche d'un des points précédemment choisis.

 

ANNEXE 4

Les calculs de J.F. Gilles ont été recommencés par M. Maurice Chatelain* et publiés par ce dernier dans un livre dont la traduction française s'intitule "Les messagers du Cosmos" ( Ed. Laffont ).

(*) Maurice Chatelain est un français résidant et travaillant aux Etats-Unis. Il est connu des milieux ufologiques car il meut s'honorer ( comme J.F. Gilles ) de certaines références scientifiques ( il travailla pour la NASA au problème des transmissions à l'occasion du programme APOLLO ).

Ces calculs utilisent les mêmes raisonnements géométriques que J.F. Gilles ( égalité des arcs de grand cercle à une incertitude près ) et s'appliquent à l'échantillon noté J.F.G. pour la France et à un échantillon américain de 76 points.

Les résultats sont présentés de la façon suivante :

"Nombre moyen de triangles isocèles obtenus avec 2 ordinateurs différents"
Nbre de points Type de points Californie New Jersey Moyenne
76 Français 419 417 418
76 Américains 133 133 133
76 Aléatoire 96 98 97

Des résultats sont aussi donnés pour des réductions de ces échantillons ( 66 points, 56 points, etc... ) mais il n'est fait nulle part mention de la façon dont ont été effectuées les ( ou la ? ) simulations ( nombre de tirages aléatoires, contour, et surface des modèles de France et des Etats-Unis ).
De plus, il n'est fourni aucune estimation de l'écart type. En conséquence de quoi, aucune signification statistique ne peut être allouée à ces résultats.

Par ailleurs, M. Chatelain nous fit parvenir son programme de calcul des triangles sphériques et ses tests "isocélarité". L'erreur absolue admise est de 1/100 de degré d'arc ( i.e. 1,11 km pour une Terre sphérique de 40 000 km de circonférence de grand cercle ).Aucune élimination de points agrégés n'y était effectuée.

En utilisant la même erreur de 1,11 km et le modèle de France précédent ( FCNES ) nous avons trouvé les résultats suivants :

  • Echantillon J.F.G. :
    Nbre de triangles isocèles : 806

  • 16 tirages aléatoires avec F.CNES :
    Nbre de triangles isocèles : 766.13
    Ecart type : 57.62
    Probabilité que le nbre de triangles isocèles soit > à 806 : 0.24

Notons qu'une élimination des triangles dont un côté serait inférieur à 10 km, conduirait à une probabilité supérieure à celle trouvée ici, comme il a été montré au paragraphe 3.2.2.2.

La nette différence du nombre de triangles isocèles trouvé dans J.F.G. ( 417 pour Chatelain, contre 806 pour le GEPAN ) s'explique aisément par les différences constatées entre les tests "d'égalité" des côtés des triangles :

  • M. Chatelain raisonne sur l'égalité des valeurs entières obtenues par troncature ou arrondi ( ce n'est pas précisé ) des arcs de grands cercles, multipliés par le facteur 100 ;

  • Le GEPAN compare la valeur absolue de la différence de ces longueurs d'arcs à l'erreur admise.

Dans le cas d'une troncature ou d'arrondi en valeur entière, l'intervalle conduisant à l'égalité a pour longueur l'erreur ( 1/100 de degré ). Dans le cas du GEPAN, cette longueur est égale à deux fois l'incertitude ( ± 1.11 km ).

Remarquons enfin la forte différence entre les nombres de triangles isocèles obtenus par M. Chatelain sur les échantillons français et américains avec une mime incertitude absolue. Ceci confirme l'influence ( notée au paragraphe 3.2.2.2. ) de la surface du pays lorsqu'on travaille avec une erreur admise absolue.

Ainsi, les calculs de M. Chatelain, pour autant qu'ils puissent être vérifiés, confirment pleinement les conclusions du GEPAN quant à l'absence de signification statistique du nombre de triangles isocèles formés par les points d'observation.

 

ANNEXE 5

Le choix du titre de ce chapitre a posé problème au GEPAN, en raison de l'abondance des formulations possibles.

C'est pourquoi, nous avons finalement décidé d'en proposer plusieurs en annexe, le lecteur restant libre d'opter à sa guise parmi cet ensemble.

TITRES POSSIBLES :

  • Quand la géométrie plane ...

  • Figure d'un mythe et/ou mythe d'une figure

  • Isocélie - Mythocélie

  • Le Triangle des Bermudes est-il isocèle ?

  • Illusions d'une méthodologie Statistique Absurde

  • Inconsistance et Médiocrité en Statistiques Appliquées

  • etc...

Bien entendu, chacun est libre de compléter cette liste en fonction de l'inspiration du moment.

BIBLIOGRAPHIE

(BES-80)   

BESSE Ph.
"Etude comparative des résultats statistiques élémentaires relatifs aux observations de phénomènes aérospatiaux non identifiés"
Note Technique n' 2, CNES/GEPAN, 1980
 
(FIG-79)

FIGUET M. & RUCHON JL.
"OVNI : le premier dossier complet des rencontres rapprochées en France"
Alain LEFEUVRE, Nice, 1979
 
(FCM-78)

FUMOUX JC.
"Les atterrissages d'OVNI : une logique de triangulation ?"
Les extra-terrestres, n° 5, janvier 1978
 
(GIL-80)

GILLE JF.
"L'isocélie - premiers résultats"
Document ronéoté, 1980
 
*(MIC-58)

MICHEL A.
"Mystérieux objets célestes"
Arthaud, Paris, 1958
 
*(MIC-70)

MICHEL A.
"Orthoténie : réalité et illusions"
Phénomènes spatiaux, n° 26, décembre 70
 
*(SAU-72)

SAUNDERS DR.
"BAVIC est-il remarquable ?"
Phénomènes spatiaux, n° 31, mars 72
(article présentant une bibliographie détaillée)
 
(SAP-78)

SAPORTA G.
"Théories et méthodes de la Statistique"
Ed. Techniq - 1978
 
*(TOU-67)

TOULET F.
"mathématiques de l'orthoténie"
Phénomènes spatiaux, n° 12, juin 67
 
*(TOU-70)

TOULET F.
"L'orthoténie n'est-elle qu'une hypothèse ?"
Phénomènes spatiaux, n° 26, décembre 70
 
*(T0U-72)

TOULET F.
"Le point de vue contre"
Phénomènes spatiaux, n° 31, mars 72
 
*(VAL-66)

VALLEE J. & VALLEE J.
"Challenge to Science"
Regnery, Chicago,1966
 

(*) Références relatives à l'orthoténie.

SUITE...

© CNES